LOS NÚMEROS ENTEROS.

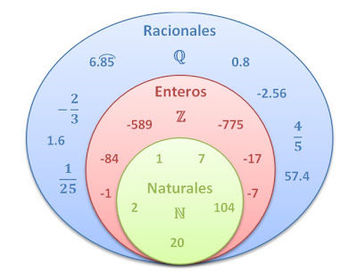
Se conoce como números enteros o simplemente enteros al conjunto numérico que contiene a la totalidad de los números naturales, a sus inversos negativos y al cero. Este conjunto numérico se designa mediante la letra Z, proveniente del vocablo alemán zahlen (“números”).

Los números enteros se representan en una recta numérica, teniendo el cero en medio y los números positivos (Z+) hacia la derecha y los negativos (Z-) a la izquierda, ambos lados extendiéndose hasta el infinito. Normalmente se transcriben los negativos con su signo (-), cosa que no hace falta para los positivos, pero puede hacerse para resaltar la diferencia.

De esta manera, los enteros positivos son mayores hacia la derecha, mientras que los negativos son cada vez más pequeños a medida que avanzamos a la izquierda. También puede hablarse del valor absoluto de un número entero (representado entre barras |z|), que es equivalente a la distancia entre su ubicación dentro de la recta numérica y el cero, independientemente de su signo: |5| es el valor absoluto de +5 o -5.

• Los Números Enteros (Z): son aquellos que poseen las siguientes características
• Incluye a los números naturales
• Incluye al cero
• Incluye los opuestos negativos de los números naturales 
• No tienen parte decimal
• No tienen parte imaginaria    

Ejemplos de Números Enteros: Z = [...-5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5...]

Tipos de números enteros:

Números Negativos: son aquellos números menores de cero: -10, -5,1 - e, 0,00233...

Números Pares: son números enteros que son divisibles entre dos. Siguen la expresión 2 · k donde k es un número entero. Algunos ejemplos son: ... -6, -4, -2, 0, 2, 4, 6...

Números Impares: son los números enteros que no son pares. Siguen la expresión 2·k-1. Algunos ejemplos son: ...-5, -3, -1, 1, 3, 5...

 LOS NÚMEROS COMPLEJOS.

Los números complejos son combinaciones de números reales y números imaginarios.

En otras palabras, los números complejos son números que tienen una parte real y una parte imaginaria.

Esquema de los números complejos.

Entonces, sabiendo que dentro de los números complejos encontramos los números reales y los números imaginarios, es más fácil comprender que los números complejos son combinaciones de números reales y números imaginarios. ¡Podemos combinarlos de las formas que queramos!

Cuando pensemos en números complejos, debemos pensar en el adjetivo de “completo” más que en el adjetivo de “complicado”. Completo en el sentido que comprende ambos mundos: el real y el imaginario.

Los Números Complejos (C): son aquellos que poseen las siguientes características

- Poseen una parte real

- Poseen una parte imaginaria

-Los Números Complejos se pueden representar el plano complejo.

-En dicho plano complejo, los valores reales están representados en el eje horizontal y los valores imaginarios en el eje vertical.

 LOS NÚMEROS RACIONALES.

Los números racionales son las fracciones que pueden formarse a partir de números enteros y pertenecen a la recta real.

Los números racionales son aquellos números que pueden ser expresados como una relación entre dos enteros. Por ejemplo, las fracciones 1/3 y -1111/8 ambas son números racionales. Todos los enteros están incluídos en los números racionales, ya que cualquier entero z puede ser escrito como la relación z /1.

Los números que no pueden ser escritos como una relación de enteros son llamados irracionales .

Todos los decimales que terminan son números racionales (ya que 8.27 puede ser escrito como 827/100.) Los decimales que tienen un patrón repetitivo después de algún punto también son racionales: por ejemplo, 0.083333333... = 1/12.

El conjunto de números racionales esta cerrado bajo las cuatro operaciones básicas: esto es, dados cualesquiera dos números racionales, su suma, diferencia, producto, y cociente también es un número racional (siempre que no dividamos entre 0.)

Tipos de números racionales

Los números reales se dividen entre números irracionales y números racionales, los cuales pueden reducirse a números enteros y estos a números naturales. Es decir, que existen dos grandes tipos de números racionales: los enteros y los naturales. 

 La Parábola. 

La Parábola es una curva abierta formada por dos líneas simétricas respecto de un eje y en que todos sus puntos están a la misma distancia del foco (punto fijo) y de la directriz (recta perpendicular al eje).

La parábola es una curva que tienen una gran importancia en Física y que se ajusta a la descripción o a la representación matemática de muchos fenómenos, también tiene importancia en nuestra vida cotidiana y, aunque muchas veces no nos fijemos o no seamos conscientes de ello, tenemos muchas parábolas a nuestro alrededor.

Por ejemplo: 

Cualquier cuerpo lanzado al aire de forma oblicua u horizontal describe un movimiento parabólico bajo la acción de la gravedad. Por ejemplo es el caso de una pelota que se desplaza botando.

ELEMENTOS DE UNA PARÁBOLA.

Foco: Es el punto fijo.

 

Vértice: Es el punto de intersección de la parábola con su eje.

Eje de simetría (focal): Es la recta perpendicular a la directriz que pasa por el foco.

Directriz: Es la recta fija perpendicular al eje de simetría (focal).

 

Parámetro: Es la distancia del foco a la directriz.

 

Eje de simetría (focal): Es la recta perpendicular a la directriz que pasa por el foco.

 

Lada recto: Es el segmento de recta comprendido por la parábola, que pasa por el foco y es paralelo a la directriz.

LA ELIPSE.

La elipse es el lugar geométrico de los puntos del plano cuya suma de distancias a dos puntos fijos llamados focos es constante.

Elementos de la elipse.

1. Focos: Son los puntos fijos F y F'.

2. Eje focal: Es la recta que pasa por los focos.

3. Eje secundario: Es la mediatriz del segmento FF'.

4. Centro: Es el punto de intersección de los ejes.

5. Radios vectores: Son los segmentos que van desde un punto de la elipse a los focos: PF y PF'.

6. Distancia focal: Es el segmento de longitud 2c, c es el valor de la semidistancia focal.

7. Vértices: Son los puntos de intersección de la elipse con los ejes: A, A', B y B'.

8. Eje mayor: Es el segmento de longitud 2a, a es el valor del semieje mayor.

9. Eje menor: Es el segmento de longitud 2b, b es el valor del semieje menor.

10. Ejes de simetría: Son las rectas que contienen al eje mayor o al eje menor.

11. Centro de simetría: Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.

 

Teorema de Pitágoras. 

El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos. Es la proposición más conocida entre las que tienen nombre propio en la matemática.

En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Un poco de historia...

El teorema de Pitágoras fue comprobado en el siglo VI a.C. por el filósofo y matemático griego Pitágoras, pero se estima que pudo haber sido previo a su existencia, o demostrado bajo otra denominación.

Respecto de los babilonios hay esta nota:

Desde el punto de vista matemático, las novedades más importantes que registran los textos babilónicos se refieren a la solución algebraica de ecuaciones lineales y cuadráticas, y el conocimiento del llamado "teorema de Pitágoras" y de sus consecuencias numéricas.

El teorema de Pitágoras tiene este nombre porque su demostración, sobre todo, es esfuerzo de la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación. 2 La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.

 Resta de polinomios.

La resta o sustracción de monomios y polinomios es una operación en la cual se quiere encontrar la diferencia entre el minuendo y el sustraendo. Para reforzar el conocimiento de la resta es importante tener los conceptos básicos en aritmética.

En la resta de monomios en realidad consiste en cambiar el signo del sustraendo, es recomendable analizar con paréntesis ya que en la resta de polinomios el signo de la resta afecta a todo el sustraendo, por lo tanto, se estaría empleando el mismo método realizado.

La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.

También podemos restar polinomios escribiendo el opuesto de uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.