Teorema de Pitágoras. 

El teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las respectivas longitudes de los catetos. Es la proposición más conocida entre las que tienen nombre propio en la matemática.

En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Un poco de historia...

El teorema de Pitágoras fue comprobado en el siglo VI a.C. por el filósofo y matemático griego Pitágoras, pero se estima que pudo haber sido previo a su existencia, o demostrado bajo otra denominación.

Respecto de los babilonios hay esta nota:

Desde el punto de vista matemático, las novedades más importantes que registran los textos babilónicos se refieren a la solución algebraica de ecuaciones lineales y cuadráticas, y el conocimiento del llamado "teorema de Pitágoras" y de sus consecuencias numéricas.

El teorema de Pitágoras tiene este nombre porque su demostración, sobre todo, es esfuerzo de la escuela pitagórica. Anteriormente, en Mesopotamia y el Antiguo Egipto se conocían ternas de valores que se correspondían con los lados de un triángulo rectángulo, y se utilizaban para resolver problemas referentes a los citados triángulos, tal como se indica en algunas tablillas y papiros. Sin embargo, no ha perdurado ningún documento que exponga teóricamente su relación. 2 La pirámide de Kefrén, datada en el siglo XXVI a. C., fue la primera gran pirámide que se construyó basándose en el llamado triángulo sagrado egipcio, de proporciones 3-4-5.

 Resta de polinomios.

La resta o sustracción de monomios y polinomios es una operación en la cual se quiere encontrar la diferencia entre el minuendo y el sustraendo. Para reforzar el conocimiento de la resta es importante tener los conceptos básicos en aritmética.

En la resta de monomios en realidad consiste en cambiar el signo del sustraendo, es recomendable analizar con paréntesis ya que en la resta de polinomios el signo de la resta afecta a todo el sustraendo, por lo tanto, se estaría empleando el mismo método realizado.

La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.

También podemos restar polinomios escribiendo el opuesto de uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.

 Suma de polinomios.

Para realizar la suma de dos o más polinomios, se debe sumar los coeficientes de los términos cuya parte literal sean iguales, es decir, las variables y exponentes (o grados) deben ser los mismos en los términos a sumar.

Métodos para sumar polinomios.

1 Ordenar los polinomios del término de mayor grado al de menor.

2 Agrupar los monomios del mismo grado.

3 Sumar los monomios semejantes.

4 También podemos sumar polinomios escribiendo uno debajo del otro, de forma que los monomios semejantes queden en columnas y se puedan sumar.

Polinomio.

¿Qués es un polinomio?

Un polinomio es una expresión algebraica de sumas, restas y multiplicaciones ordenadas hecha de variables, constantes y exponentes.

En álgebra, un polinomio puede tener más de una variable (x, y, z), constantes (números enteros o fracciones) y exponentes (que solo pueden ser números positivos enteros).

Tipos de polinomio:

La cantidad de términos que un polinomio tiene indicará qué tipo de polinomio es, por ejemplo,

Polinomio de un término: monomio, por ejemplo, 8xy.

Polinomio de dos términos: binomio, por ejemplo, 8xy - 2y.

Polinomio de tres términos: trinomio, por ejemplo, 8xy - 2y + 4.

Grado de polinomio.

El grado de un polinomio de una sola variable es el mayor exponente. El grado de un polinomio con más de una variable es determinado por el término con el mayor exponente. Por ejemplo: el polinomio 3x+8xy+7x2y

3x: grado 1

8xy: grado 2 (x:1 + y:1= 2)

7x2y:grado 3 (x:2 + y:1=3)

Esto significa que el grado del polinomio es 3 siendo el mayor exponente de los tres términos que lo componen

Partes de un polinomio.

 

Sistemas de numeración.

NUMERACIÓN EGIPCIA

La numeración egipcia es uno de los sistemas más antiguos. El sistema de numeración egipcia permitía representar números, desde el 1 hasta l millones. El orden en el que acomodaban los símbolos no era tan importante, ya que cada símbolo tenía un único valor y era fácil reconocer a que número se estaba refiriendo, por ello no necesitaron el cero.

 NUMERACIÓN BABILONICA.

Este sistema de numeración se llevó a cabo en Mesopotamia por primera vez entre los años 1800-1900ª. C el cual es muy representativo entre la escritura de números de manera cuneiforme como lo son los sumerios y los alcaldios. Al sistema babilónico se le acredita el ser el primer sistema numérico posicional ya que obligaba a usar símbolos únicos para representar cada potencia de una base. Aun teniendo un sistema decimal interno se prefirió tomar el 60 como la segunda mitad más pequeña en lugar de 100 como actualmente, es considerado un sistema mixto de las bases 10 y 60. De esto se deriva el uso actual de 60 segundos en un minuto, 60 minutos en una hora. 360 grados en un círculo, etc.

NUMERACIÓN CHINA.

Es un sistema de numeración posicional, multiplicativo y de base 10. Y también usaban un ábaco para las operaciones.

Su numeración está formada por 14 signos fundamentales que designan las nueve unidades y las primeras cinco potencias de 10. Los números se obtienen combinado estos números.

Por otra parte, el sistema de numeración chino es, además, un sistema de numeración aditivo ya que se basa en acumular los símbolos de todas las unidades, decena y centenas como sean necesarios hasta completar el número. Una de sus características es por tanto que se pueden poner los símbolos en cualquier orden, aunque en general se haya preferido una determinada disposición.

  NUMERACIÓN MAYA.

Los mayas fueron una de las civilizaciones más importantes y estaban ubicados en Mesoamérica, una de las cunas de las civilizaciones más importantes del mundo.

En cuanto al sistema de numeración y los números mayas en sí, cabe destacar que los mayas inventaron un sistema de numeración como modo de instrumento para medir el tiempo y no para hacer cálculos matemáticos, a diferencia de muchas otras civilizaciones.

Los tres símbolos básicos eran el punto que equivale al uno, la raya que su valor es el cinco y el caracol (también conocido como concha o semilla) es valor cero. Combinando estos símbolos se obtenían los números del 0 al 20

Para escribir los números del 20 en adelante se hacia lo siguiente: En el nivel inferior van los numerales, que son los números del 0 al 20. En el nivel superior cualquier número que se coloque vale esta cifra multiplicada por 20.

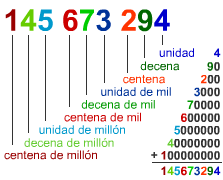
NUMERACIÓN DECIMAL

Según los antropólogos, el origen del sistema decimal está en los diez dedos que tienen los hombres en las manos que siempre han servido como base para contar. También existen algunos vestigios del uso de otros sistemas de numeración, como el quinario, el duodecimal y el vigesimal. El desarrollo de las cifras del uno al nueve, se hizo en la India según las Inscripciones De Nana Ghat en el siglo III a. C. sin sistema de posición de ellas. esto último hace su primera aparición en el año 458 en el documento Lokavibhaga, un tratado de cosmología escrito en sánscrito. Aparece el número 14 236 713 y el cero, el vacío donde ocupan la palabra sunya.Más tarde este sistema lo toman los árabes cambiando el aspecto de las cifras llamadas ghobar en las cifras que usamos hoy en día 1,2,3,4,5,6,7,8,9,0.

 

NUMERACIÓN ROMANA.

Los romanos utilizaron letras mayúsculas para representar cantidades. Estas letras que utiliza equivalen a un número específico en la numeración decimal. Las letras que utilizaron y sus valores son las siguientes:

En la actualidad se sigue utilizando esta numeración en casos específicos, como por ejemplo para escribir fechas (siglo XXI), para numerar capítulos de obras (Capítulo V), para designar nombre de algunas autoridades (Papa II, Rey XV), etc.

Hay límites para escribir cantidades en números romanos, no se pueden utilizar más de dos o tres veces, el número más grande que se puede escribir es el 3999 que se escribe MMMCMXCIX. Para expresar cantidades mayores a este se coloca una rayita arriba de la letra y esta indica lo que vale multiplicando por 1000, dos rayitas encima indican tantos millones como unidades tenga el símbolo y se multiplica por 1,000,000.

 

NUMERACIÓN GRIEGA

El primer sitema de numeración griego se desarrolló hacia el 600 A.C. Era un sistema de base decimal que usaba los símbolos de la figura siguiente para representar esas cantidades. Se utilizaban tantas de ellas como fuera necesario según el principio de las numeraciones aditivas.

Para representar la unidad y los números hasta el 4 se usaban trazos verticales. Para el 5, 10 y 100 las letras correspondientes a la inicial de la palabra cinco (pente), diez (deka) y mil (khiloi). Por este motivo se llama a este sistema acrofónico.

 

 

Sistema de numeración unario

El sistema de numeración unario es un sistema de numeración biyectivo de base 1. Es el sistema de numeración más simple que existe para representar los números naturales. Para representar un número N, se elige un símbolo arbitrario, que será la única cifra que tenga dicho sistema de numeración, y se repetirá N veces. Por ejemplo, si tomamos el símbolo | como cifra única, el número 6 se representará como ||||||. El sistema tradicional de contar con los dedos es un ejemplo de numeración unaria. El sistema unario es útil en procesos de conteo, como el marcador de un deporte, o contar el número de personas que entran en un lugar, o el número de votos que van saliendo en una elección, ya que no requiere ir enmendando los resultados previos, simplemente hay que seguir añadiendo símbolos para su posterior recuento.

 

Ejemplos de este sistema.

Las marcas se suelen agrupar frecuentemente en grupos de cinco para que sea más legible y sencillo el recuento posterior. Cuando el símbolo utilizado es una raya (el más frecuente) es común atravesar la quinta línea sobre las cuatro previas para formar grupos. En los sistemas de numeración chino, japonés y coreano se agrupan los símbolos se van añadiendo hasta que el quinto cierra el grupo y forma un símbolo que significa cinco.

 

Otro método utilizado en Argentina, Brasil y también en Francia es ir dibujando las líneas formando los lados de un cuadrado. Uno se representa con una línea vertical, el dos formaría con ésta una L, el tres formaría una U junto a ellos, el cuatro cerraría el cuadrado y el cinco se añadiría en una de las diagonales del mismo.

Existen multitud de sistemas de numeración antiguos que, sin ser unarios, provienen claramente de sistemas de este tipo:

Los tres primeros números del sistema de numeración romano (hasta el cuatro en los relojes) se basan en el sistema de numeración unario.

El sistema de numeración egipcio utiliza el sistema unario para números del uno al diez, después utiliza un número para el diez, que repite como si fuera un sistema unario para los números del diez al noventa. Así sucesivamente, tiene símbolos para 1, 10, 100, 1000, 10.000, 100.000 y hasta 1.000.000 que repite y conjunta para formar números.

Ventajas e inconvenientes del sistema de numeración.

La suma y resta de números en sistema unario se hacen simples, ya que sólo consiste en juntar dos números o tachar símbolos. Sin embargo, la multiplicación y división en este sistema resultan bastante complicados.

Por su definición, no se puede representar el número cero en este sistema. Si se introdujera cualquier símbolo para representar al cero, eso convertiría al sistema en un sistema de numeración binario. Esto caracteriza, por ejemplo, al sistema de numeración romano, que es incapaz de representar la ausencia de algo, lo cual es un inconveniente grande para la Matemática y su desarrollo.

 

Historia de los números naturales.

Antes de que surgieran los números naturales para la representación de cantidades, las personas usaban otros métodos para contar, utilizando para ello objetos como piedras, palitos de madera, nudos de cuerdas, o simplemente los dedos. Más adelante comenzaron a aparecer los símbolos gráficos como señales para contar, por ejemplo, marcas en una vara o simplemente trazos específicos sobre la arena. Pero fue en Mesopotamia alrededor del año 400 a. C. donde aparecen los primeros vestigios de los números que consistieron en grabados de señales en forma de cuñas sobre pequeños tableros de arcilla empleando para ello un palito aguzado. De aquí el nombre de escritura cuneiforme. Este sistema de numeración fue adoptado más tarde, aunque con símbolos gráficos diferentes, en la Grecia Antigua y en la Antigua Roma. En la Grecia antigua se empleaban simplemente las letras de su alfabeto, mientras que, en la antigua Roma, además de las letras, se utilizaron algunos símbolos.

Quien colocó al conjunto de los números naturales sobre lo que comenzaba a ser una base sólida, fue Richard Dedekind en el siglo XIX. Este los derivó de una serie de postulados (lo que implicaba que la existencia del conjunto de números naturales se daba por cierta), que después precisó Peano dentro de una lógica de segundo orden, resultando así los famosos cinco postulados que llevan su nombre. Frege fue superior a ambos, demostrando la existencia del sistema de números naturales partiendo de principios más fuertes. Lamentablemente la teoría de Frege perdió, por así decirlo, su credibilidad, y hubo que buscar un nuevo método. Fue Zermelo quien demostró la existencia del conjunto de los naturales, dentro de su teoría de conjuntos y principalmente mediante el uso del axioma de infinitud, que, con una modificación de este hecha por Adolf Fraenkel, permite construir el conjunto de números naturales como ordinales según von Neumann.

En matemáticas, un número natural es cualquiera de los números que se usan para contar los elementos de ciertos conjuntos, ​como también en operaciones elementales de cálculo. Los números naturales son aquellos que sirven para contar elementos enteros, por ejemplo: 5,7,8,9… Por definición convencional se dirá que cualquier elemento del siguiente conjunto, ℕ = {1, 2, 3, 4, …}, es un número natural. ​ En obras más modernas, aparece también como ℕ = {0, 1, 2, 3, 4, …}.​ De dos números vecinos, el que se encuentra a la derecha se llama siguiente o sucesivo, por lo que el conjunto de los números naturales es ordenado e infinito.

 

Propiedades de la suma
 

Propiedad 1.  la cerradura

"La suma de dos naturales es otro natural"

Ejemplo:

5+7=12

Propiedad 2. Conmutatividad.

“Dos números naturales pueden cambiar su orden sin alterar la suma”

Para todos a y b que pertenecen a los números naturales se cumple que a+b=a+b

Ejemplo:

3+8=8+3

Propiedad 3. Asociatividad.

“podemos agrupar números de cualquier forma y el resultado es el mismo”

Ejemplo:

(5+7)+4=5+(7+4)

En ciertas ocasiones podemos mezclar la propiedad conmutativa y asociativa.

Propiedad 4. Cancelativa.

“sean a,b,c pertenecen a los naturales. Si a+c=b+c entonces a=b. si agregamos la misma cantidad a ambos lados la igualdad se mantiene”.

 

Ejemplo:

a+10=15+10

a= 15

Propiedad 5. Inverso aditivo.

“Si a un número lo restamos así mismo el resultado es cero”

Ejemplo:  11-11=0

Propiedad 6. Elemento neutro aditivo.

“Si a un número se le suma 0 el resultado es el mismo número”

Ejemplo: 7+0=0+7

Video.

 

Propiedades de la multiplicación.
 

Los números naturales son un conjunto cerrado para la multiplicación, lo que significa que cuando multiplicamos dos números naturales, el resultado sigue siendo un natural, de esto se deducen las siguientes propiedades.

Conmutativa. 

El orden de los factores no altera el producto

a*b=b*a

 

Asociativa. 

El producto puede cambiar su oren de asociación sin alterar el resultado.

a*(b*c)=(a*b)*c

 

Distributiva.

El producto puede distribuirse sobre una suma sin alterar el resultado.

a*(b+c) = a*b + a*c

 

Elemento neutro. 

Al multiplicar por 1 cualquier natural, el resultado sigue siendo el mismo número natural.

a*1 = a

El cero como absorbente. 

Todo numero multiplicado por cero es cero.

a*0 = 0

 

 Las operaciones básicas de matemática.

Las operaciones básicas de matemática son cuatro:

•  Suma

 

• Resta

 

• Multiplicación

 

•   División.

La suma.

Como operación matemática, la suma o adhesión consiste en añadir dos números o más para obtener una cantidad total.

Se representa por el signo:

Ejemplo:

2+3=5

6+8=14

La resta. 

La resta, también conocida como sustracción, es una operación que consiste en sacar, recortar, empequeñecer, reducir o separar algo de un todo.

Se representa por el signo.

                                 

Ejemplos

6-2=4

8-5=3

La multiplicación. 

La multiplicación es aquella operación mediante la cual se suma un número por si mismo tantas veces como lo señala otro numero.

Se representa por el signo.

Ejemplos

3x4=12

3x5=15

La división.

La división es aquella operación matemática mediante la cual se trata de descomponer un número, al que denominaremos dividendo, en tantas partes como así lo indique otro número, al que llamaremos divisor.

Se representa por el signo.

Ejemplos.

72÷9=8

36÷4=9